| Latest Maths NCERT Books Solution | ||||||
|---|---|---|---|---|---|---|
| 6th | 7th | 8th | 9th | 10th | 11th | 12th |
Chapter 8 Playing with Constructions
Welcome to the solutions guide for Chapter 8, "Playing with Constructions," a hands-on exploration of practical geometry featured in the Class 6 Ganita Prakash textbook (NCERT, 2024-25 session). This chapter shifts the focus from theoretical understanding to the precise art of drawing geometric figures using fundamental tools. These solutions are designed to provide highly detailed, sequential instructions, acting as a virtual tutor guiding students through the essential techniques of using a ruler (straightedge) and a pair of compasses to create accurate geometric constructions.
The essence of this chapter lies in appreciating the power and precision offered by these simple instruments. Unlike freehand sketching, geometric constructions demand accuracy, achieved through the careful use of a ruler for drawing straight line segments and measuring lengths, and compasses for drawing arcs and circles, and crucially, for transferring lengths accurately without direct measurement. The solutions emphasize the correct handling of these tools – maintaining a sharp pencil point in the compasses, setting the radius accurately, and drawing clear arcs – as foundational to successful construction. This chapter builds spatial reasoning and an understanding of geometric properties through action.
These solutions meticulously detail the steps required for several fundamental constructions involving lines and angles. Key constructions covered include:
- Constructing a line segment of a precisely given length.
- Copying a given line segment accurately onto another position without measuring its length directly, using only compasses and a ruler.
- Constructing a line perpendicular to a given line, addressing two scenarios: through a point situated on the line itself, and from a point located outside the line.
- Constructing the perpendicular bisector of a given line segment. The solutions highlight how this construction simultaneously finds the midpoint of the segment and creates a line at a perfect $90^\circ$ angle to it.
Furthermore, the solutions provide comprehensive guidance on constructions related to angles:
- Copying a given angle: Transferring an angle of unknown measure to a different location using only compass and ruler techniques.
- Bisecting a given angle: Dividing an angle into two angles of exactly equal measure (finding $\frac{\theta}{2}$ if the original angle is $\theta$).
- Constructing specific angles using only ruler and compasses (without a protractor). This often involves leveraging properties of equilateral triangles (for $60^\circ$) and bisection techniques. Common constructions explained include: $60^\circ$, $120^\circ$ (as $2 \times 60^\circ$), $90^\circ$ (often by bisecting a straight angle, $180^\circ$, or constructing a perpendicular), $30^\circ$ (by bisecting a $60^\circ$ angle), and $45^\circ$ (by bisecting a $90^\circ$ angle).
The emphasis throughout these solutions for Chapter 8 of the Class 6 Ganita Prakash (NCERT 2024-25) is not just on achieving the final figure, but on understanding the process and the underlying geometric principles that make these constructions work. By carefully following these detailed, step-by-step solutions, students will develop essential dexterity with geometric tools, enhance their fine motor skills and spatial awareness, and gain a deeper appreciation for how precise geometric figures can be created based purely on logical steps and the properties of shapes, laying a strong foundation for future geometry studies.
Construct (Page 190 - 191)
Question 1. A Person
How will you draw this?
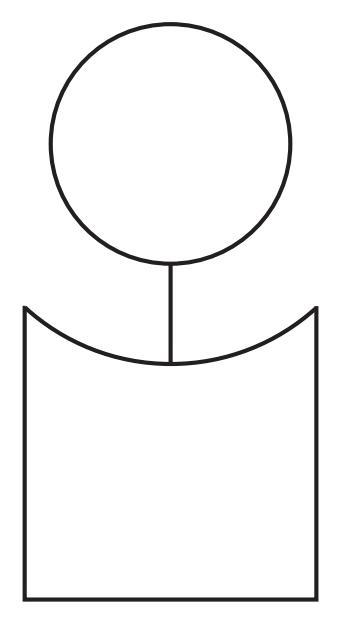
This figure has two components.
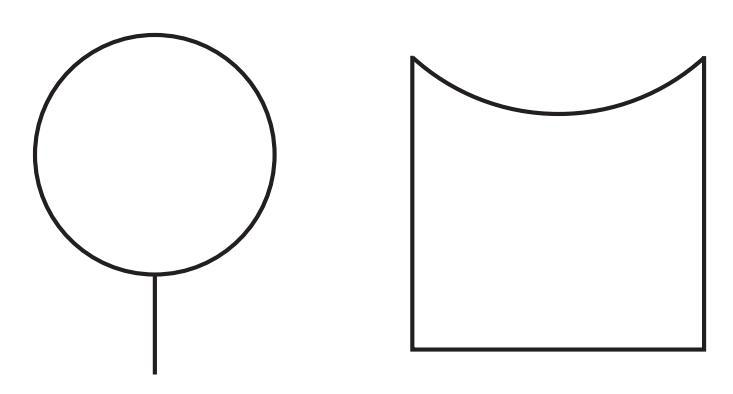
You might have figured out a way of drawing the first part. For drawing the second part, see this.
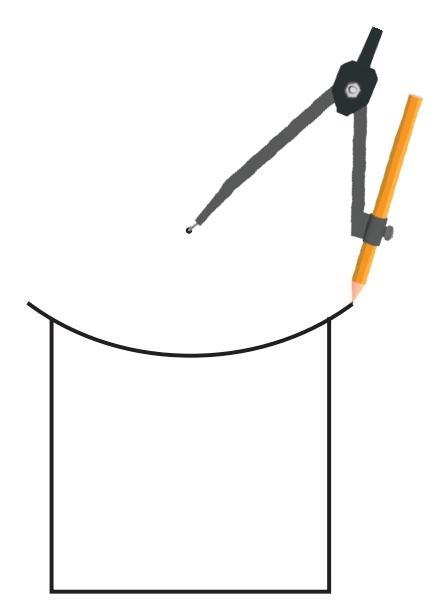
The challenge here is to find out where to place the tip of the compass and the radius to be taken for drawing this curve. You can fix a radius in the compass and try placing the tip of the compass in different locations to see which point works for getting the curve. Use your Estimate where to keep the tip.
Answer:
To draw this figure of a person using geometric tools like a ruler and compass, we can break it down into its basic shapes: line segments (for the body and limbs) and curves (for the head and feet/legs).
Steps for Construction:
1. Draw the Body: Draw a vertical line segment for the main body. Let's call the top point A and the bottom point B.
2. Draw the Head: The head is a circle. Place the tip of your compass at point A and open the compass to a desired radius (this will determine the size of the head). Draw a circle centered at A. This is the head.
3. Draw the Arms and Legs: Draw line segments starting from points on the main body (point A or a point slightly below it for arms, and point B for legs). The arms can be single line segments. The legs can be drawn as line segments extending downwards from B.
4. Draw the Feet/Leg Curves: This is the challenging part involving curves. The image shows a curve extending from the bottom of the leg. To draw this curve using a compass (which draws arcs of circles), you need to find the center and the radius of the circle of which this curve is a part.
Let the bottom of the leg segment be point C. The curve starts near C and ends at some point D (representing the toe). The curve looks like an arc of a circle.
As suggested in the question, you need to estimate the center of the circle and its radius.
Place the tip of your compass at a point that you estimate to be the center of the arc. Let's call this estimated center O. This point O will likely be somewhere to the side and slightly above the starting point of the curve (point C).
Adjust the compass opening (radius) so that when the tip is at O, the pencil point can draw the required curve passing through the intended shape of the foot.
Try placing the compass tip at different points and adjusting the radius until the arc looks similar to the one in the figure.
Alternatively, you might observe that the curve looks like an arc centered somewhere near the knee or hip joint, creating a curve for the lower leg or foot. Given the diagram showing the curve from the bottom of the vertical body line, it's likely an arc for the lower leg/foot region.
To draw the curve extending from the bottom of the leg segment (say point C), estimate a center point O. The radius will be the distance from O to C, or close to it. Place the compass tip at O, set the radius to OC (or an estimated value), and draw the arc from C to the desired endpoint of the foot.
By combining straight line segments for the body and limbs, a circle for the head, and carefully estimated arcs for the feet/legs using a compass, you can construct the figure.
Question 2. Wavy Wave
Construct this.
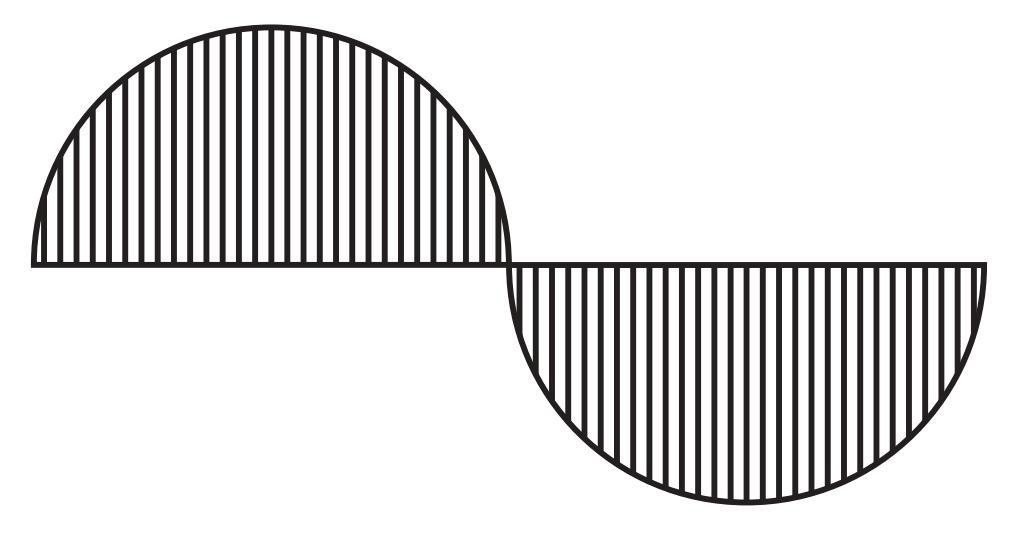
As the length of the central line is not specified, we can take it to be of any length.
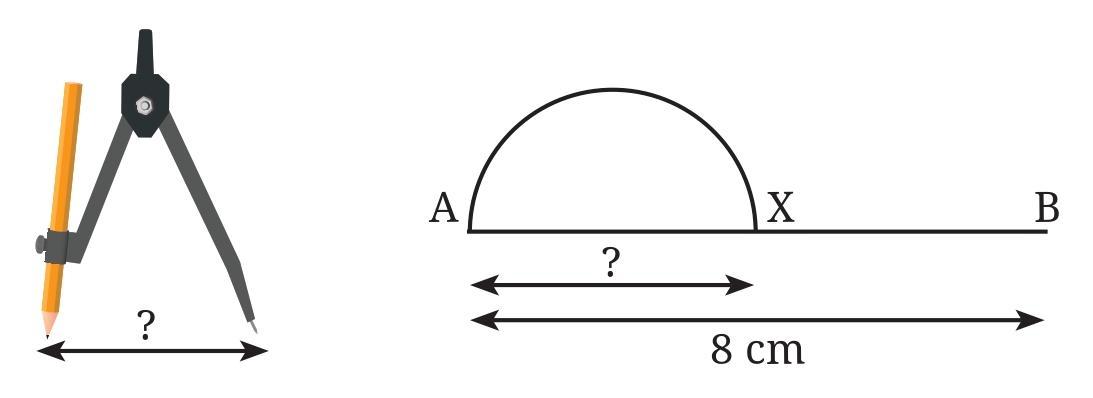
Let us take AB to be the central line such that the length of AB is 8 cm. We write this as AB = 8 cm.
Here, the first wave is drawn as a half circle.
Answer:
To construct the "Wavy Wave" figure, we need to draw a central line and then draw a series of semi-circles (half-circles) along this line, alternating above and below the line.
Based on the example given (AB = 8 cm) and the visual pattern, it appears the central line is divided into equal segments, and each segment serves as the diameter of a semi-circle. The full pattern shown consists of 8 such segments (4 complete "waves" alternating up and down).
Let's follow the suggestion and take the central line AB = 8 cm.
Steps for Construction:
1. Draw the Central Line: Use a ruler to draw a line segment AB of length 8 cm. Mark the points A and B.
2. Divide the Line Segment: Divide the line segment AB into 8 equal parts. Since the total length is 8 cm, each part will be $8 \text{ cm} \div 8 = 1 \text{ cm}$ long.
Mark the points along AB starting from A, at intervals of 1 cm. Let these points be $P_1, P_2, P_3, P_4, P_5, P_6, P_7$. Note that A can be considered as $P_0$ and B as $P_8$. So, the segments are $AP_1, P_1P_2, P_2P_3, \dots, P_7B$, each of length 1 cm.
3. Determine the Radius and Centers: Each segment $P_i P_{i+1}$ will be the diameter of a semi-circle. The length of each diameter is 1 cm. The radius of each semi-circle is half the diameter, i.e., $1 \text{ cm} \div 2 = 0.5 \text{ cm}$.
The center of the semi-circle for the segment $P_i P_{i+1}$ is the midpoint of that segment. For example, the center of the semi-circle on $AP_1$ (or $P_0P_1$) is the midpoint of $AP_1$. This point is at a distance of $0.5$ cm from A (or $P_1$).
4. Draw the Semi-circles: We draw the semi-circles one by one, alternating their direction (below/above the line AB).
- First semi-circle (on $AP_1=P_0P_1$): Find the midpoint of $AP_1$. Let it be $M_1$. This point is $0.5$ cm from A. Place the tip of the compass at $M_1$ and set the radius to $0.5$ cm. Draw a semi-circle below the line segment $AP_1$ connecting points A and $P_1$.
- Second semi-circle (on $P_1P_2$): Find the midpoint of $P_1P_2$. Let it be $M_2$. This point is $1.5$ cm from A. Place the tip of the compass at $M_2$ and set the radius to $0.5$ cm. Draw a semi-circle above the line segment $P_1P_2$ connecting points $P_1$ and $P_2$.
- Third semi-circle (on $P_2P_3$): Find the midpoint of $P_2P_3$. Let it be $M_3$. This point is $2.5$ cm from A. Place the tip of the compass at $M_3$ and set the radius to $0.5$ cm. Draw a semi-circle below the line segment $P_2P_3$ connecting points $P_2$ and $P_3$.
- Continue this alternating pattern (above, below, above, below...) for the remaining segments ($P_3P_4, P_4P_5, P_5P_6, P_6P_7, P_7B$). Find the midpoint of each segment, place the compass tip there, set the radius to $0.5$ cm, and draw the semi-circle on the appropriate side of the line.
By following these steps, you will construct the "Wavy Wave" figure consisting of 8 semi-circles (4 below and 4 above the central line segment AB).
How do you draw these eyes with a compass?
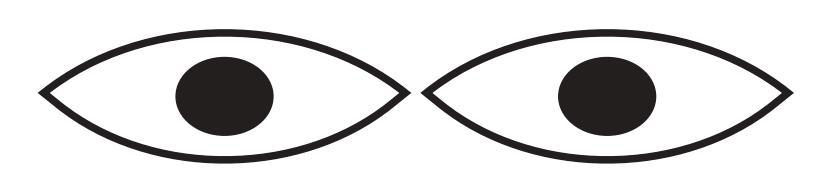
Answer:
To draw these eyes using a compass, we can see that the figure is primarily made up of circles and curves which are parts of circles (arcs).
Let's break down the process for drawing a single eye:
1. Draw the Iris and Pupil:
- First, decide where you want the center of the eye to be. Mark this point on your paper. Let's call it C.
- Set your compass to a certain radius (this will be the radius of the outer part of the iris). Place the tip of the compass on point C and draw a circle.
- Now, set your compass to a smaller radius (for the pupil). Keep the tip of the compass on the same center point C and draw a smaller circle inside the first one.
2. Draw the Highlight (Optional but adds detail):
- Choose a point within the pupil circle where you want the highlight to be (it should not be exactly at the center C). Let's call this point H.
- Set your compass to a very small radius for the highlight circle. Place the tip of the compass on point H and draw a small circle.
3. Draw the Outer Eye Shape (Eyelids):
This is the part that requires estimation, as mentioned in the question. The outer shape looks like two arcs meeting at the sides.
- Imagine or lightly mark the points where the left and right corners of the eye will be relative to your iris/pupil circles. Let's call these points E1 and E2. These points will likely be roughly level horizontally and outside the iris circle.
- For the Upper Eyelid: The curve of the upper eyelid typically arches upwards. This curve can be thought of as an arc of a circle whose center is somewhere below the imaginary line segment connecting E1 and E2. You will need to estimate where this center point should be (let's call it O_upper) and what radius (the distance from O_upper to E1 or E2) to use in your compass. Place the compass tip at your estimated center O_upper, set the radius, and draw an arc that starts at E1 and ends at E2, passing above the iris circle. You might need to try a few different positions for O_upper and adjust the radius until the arc looks right.
- For the Lower Eyelid: The curve of the lower eyelid typically curves downwards. This curve can be thought of as an arc of a circle whose center is somewhere above the imaginary line segment connecting E1 and E2. You will need to estimate where this center point should be (let's call it O_lower) and what radius (the distance from O_lower to E1 or E2) to use. Place the compass tip at your estimated center O_lower, set the radius, and draw an arc that starts at E1 and ends at E2, passing below the iris circle. Again, trial and error might be needed to get the shape correct.
4. Draw the Second Eye:
- Once you have drawn one eye, choose the position for the center of the second eye (C'). This center should be placed at a reasonable distance from the first eye (typically, the distance between the centers of the eyes is roughly equal to the width of one eye).
- Repeat steps 1-3 for the second eye, starting with the center C'. Try to make the second eye similar in size and shape to the first one.
By using the compass to draw the concentric circles for the iris and pupil, and then estimating the centers and radii for the upper and lower eyelid arcs, you can construct the pair of eyes.
Figure it Out (Page 191)
Question 1. What radius should be taken in the compass to get this half circle? What should be the length of AX?
Answer:
Given:
From the previous question (Wavy Wave), the central line AB is taken as 8 cm and is divided into 8 equal parts. The first semi-circle is drawn on the first part, which is the segment starting from A. Let's assume the points dividing the line AB are $P_1, P_2, \dots, P_7$. The first part is $AP_1$. The point X is shown as the center of the half circle drawn on $AP_1$.
To Find:
1. The radius that should be taken in the compass to get this half circle.
2. The length of AX.
Solution:
The central line AB of length 8 cm is divided into 8 equal parts.
The length of each equal part = $\frac{\text{Total length}}{\text{Number of parts}} = \frac{8 \text{ cm}}{8} = 1 \text{ cm}$.
The first semi-circle is drawn on the first part, which is the segment $AP_1$. This segment $AP_1$ serves as the diameter of the semi-circle.
Length of diameter = Length of $AP_1 = 1 \text{ cm}$.
1. The radius of a semi-circle is half of its diameter.
Radius = $\frac{1}{2} \times \text{Diameter}$
Radius = $\frac{1}{2} \times 1 \text{ cm} = 0.5 \text{ cm}$.
2. The point X is the center of the semi-circle. The center of a semi-circle lies at the midpoint of its diameter.
Therefore, X is the midpoint of the segment $AP_1$.
The length of AX is the distance from one end of the diameter (A) to its midpoint (X).
Length of AX = $\frac{1}{2} \times \text{Length of } AP_1$
Length of AX = $\frac{1}{2} \times 1 \text{ cm} = 0.5 \text{ cm}$.
Answer:
The radius that should be taken in the compass is $0.5 \text{ cm}$.
The length of AX should be $0.5 \text{ cm}$.
Question 2. Take a central line of a different length and try to draw the wave on it.
Answer:
We will take a central line of a different length and follow similar steps as before to draw the wavy wave pattern.
Let's choose the length of the central line to be 12 cm.
We will assume the pattern consists of 8 semi-circles, similar to the previous example. This means the central line needs to be divided into 8 equal parts.
Steps for Construction:
1. Draw the Central Line: Use a ruler to draw a line segment AB of length 12 cm. Mark the points A and B.
2. Divide the Line Segment: Divide the line segment AB into 8 equal parts.
The length of each equal part = $\frac{\text{Total length}}{\text{Number of parts}} = \frac{12 \text{ cm}}{8}$.
$\frac{12}{8} = \frac{12 \div 4}{8 \div 4} = \frac{3}{2} = 1.5 \text{ cm}$.
Mark the points along AB starting from A, at intervals of 1.5 cm. Let these points be $P_1, P_2, \dots, P_7$. A is $P_0$ and B is $P_8$. The segments are $AP_1, P_1P_2, \dots, P_7B$, each of length 1.5 cm.
3. Determine the Radius and Centers: Each segment $P_i P_{i+1}$ is the diameter of a semi-circle. The length of each diameter is 1.5 cm.
The radius of each semi-circle = $\frac{1}{2} \times \text{Diameter} = \frac{1}{2} \times 1.5 \text{ cm} = 0.75 \text{ cm}$.
The center of the semi-circle for the segment $P_i P_{i+1}$ is the midpoint of that segment. For example, the center for the semi-circle on $AP_1$ is the midpoint of $AP_1$. This point is at a distance of $0.75$ cm from A.
4. Draw the Semi-circles: Draw the semi-circles using a compass, alternating their direction (below/above the line AB).
- Set the compass radius to 0.75 cm.
- Find the midpoint of the first segment $AP_1$. Place the compass tip at this midpoint and draw a semi-circle below the line AB, connecting A and $P_1$.
- Find the midpoint of the second segment $P_1P_2$. Place the compass tip at this midpoint and draw a semi-circle above the line AB, connecting $P_1$ and $P_2$.
- Continue this process for the remaining segments ($P_2P_3, \dots, P_7B$), alternating the direction of the semi-circle above and below the line AB.
By following these steps with a central line of 12 cm, divided into 8 parts of 1.5 cm each, and using a compass radius of 0.75 cm centered at the midpoint of each segment, you can draw the wavy wave pattern.
Question 3. Try to recreate the figure where the waves are smaller than a half circle (as appearing in the neck of the figure ‘A Person’). The challenge here is to get both the waves to be identical. This may be tricky!
Answer:
To recreate the curves forming the neck of the "A Person" figure, which are smaller than half-circles and are identical, we will use a compass to draw arcs of circles.
The neck shape consists of two identical upward-curving arcs that meet at a central point below the head and extend downwards and outwards to the shoulders.
Steps for Construction:
1. Mark the Meeting Point: Choose a point where the two neck curves will meet, just below where the head would be placed. Let's call this point P.
2. Mark the Shoulder Points: Choose two points, one on the left (S1) and one on the right (S2), where the neck curves will end at the shoulders. To make the curves identical and the figure symmetrical, ensure that points S1 and S2 are at the same vertical distance below point P and are at equal horizontal distances from a vertical line passing through P.
Measure the distance PS1 and PS2. They should be equal (PS1 = PS2).
3. Choose a Radius for the Arcs: The curves in the figure are arcs of circles. To draw them with a compass, we need to determine the radius. The arc from P to S1 (or P to S2) will be part of a circle whose center is equidistant from P and S1 (or P and S2). For the arc to curve upwards, the center must be located below the line segment PS1 (or PS2).
Choose a radius R for the arcs. This radius R must be greater than half the distance between P and S1 (or P and S2).
Estimate a suitable radius R based on the appearance of the neck in the image. It should be a radius that gives the desired curvature – less curved than a semi-circle whose diameter is PS1.
4. Find the Center for the Left Arc: Place the tip of your compass at point P and open it to the chosen radius R. Draw an arc in the region where you expect the center of the left neck curve to be (which is below the line segment PS1).
Now, place the tip of your compass at point S1, keeping the same radius R. Draw another arc that intersects the previous arc you drew from P. The intersection point of these two arcs is the center for the left neck curve. Let's call this center C1. C1 should be located below the line segment PS1.
5. Find the Center for the Right Arc: Place the tip of your compass at point P and open it to the same radius R. Draw an arc below the line segment PS2.
Now, place the tip of your compass at point S2, keeping the same radius R. Draw another arc that intersects the arc you drew from P. The intersection point of these two arcs is the center for the right neck curve. Let's call this center C2. C2 should be located below the line segment PS2. (If S1 and S2 are chosen symmetrically, C1 and C2 will also be located symmetrically).
6. Draw the Neck Arcs:
- Place the tip of your compass at center C1 and set the radius to R. Draw the arc starting from point P and ending at point S1. This should form the left side of the neck.
- Place the tip of your compass at center C2 and set the radius to R. Draw the arc starting from point P and ending at point S2. This should form the right side of the neck.
By carefully choosing the points P, S1, and S2 symmetrically and using the same radius R to find the centers C1 and C2, you will be able to draw two identical upward-curving arcs for the neck.
Figure it Out (Page 194)
Question 1.
Draw the rectangle and four squares configuration (shown in Fig. 8.3) on a dot paper.
What did you do to recreate this figure so that the four squares are placed symmetrically around the rectangle? Discuss with your classmates.
Answer:
Given:
Figure 8.3 shows a rectangle with four squares attached symmetrically around it, drawn on a dot paper.
Task:
Recreate the figure on a dot paper and explain how symmetry is achieved.
Steps to Recreate the Figure on Dot Paper:
1. Look at the figure and determine the dimensions of the central rectangle in terms of the spacing between the dots. Count the number of units (spaces between dots) for the length and the width of the rectangle. Let's say the rectangle is 'W' units wide and 'L' units long based on the dot grid.
2. Using a pencil and ruler (or just by connecting dots), draw the central rectangle on the dot paper with the dimensions you observed (W units by L units).
3. Observe the squares attached to the rectangle. Notice that the side length of each square is equal to the length of the rectangle side it is attached to.
4. On each of the two sides of the rectangle that have length 'W', draw a square of side length 'W'. Position each square so that one of its sides lies exactly along the corresponding side of the rectangle.
5. On each of the two sides of the rectangle that have length 'L', draw a square of side length 'L'. Position each square so that one of its sides lies exactly along the corresponding side of the rectangle.
Discussion on Achieving Symmetry:
To recreate the figure so that the four squares are placed symmetrically around the rectangle, I did the following:
1. I ensured that the side length of each square matched the length of the rectangle side it was attached to. This makes the squares fit perfectly alongside the rectangle's edges.
2. I attached a square to each of the four sides of the central rectangle.
3. The term "symmetrically" in this context means that identical shapes (squares) are placed on opposite sides of the central rectangle. Since the rectangle has rotational symmetry and reflectional symmetry through the midpoints of its sides, placing a square whose side length matches the rectangle's side length directly along that side ensures symmetry.
Specifically, the squares attached to the two opposite sides of length 'W' are identical (W x W squares), and they are positioned symmetrically relative to the center of the rectangle and the midpoints of the 'L' length sides. Similarly, the squares attached to the two opposite sides of length 'L' are identical (L x L squares), positioned symmetrically relative to the center of the rectangle and the midpoints of the 'W' length sides.
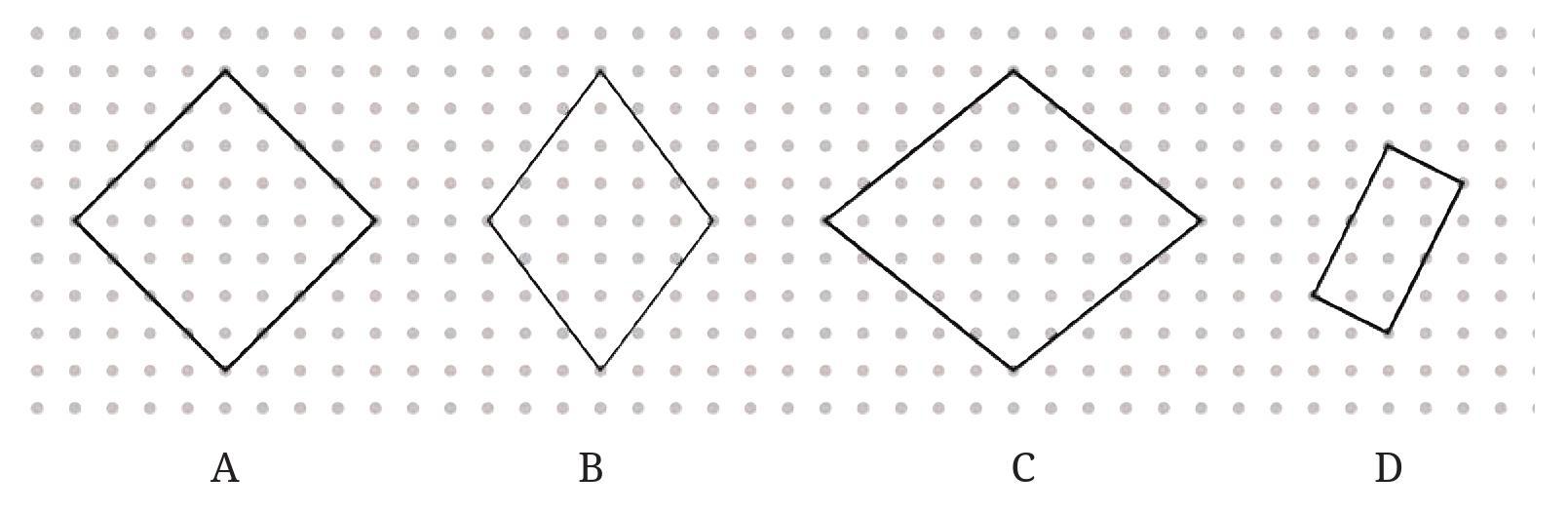
Think: Is it possible to reason out if the sides are equal or not, and if the angles are right or not without using any measuring instruments in the above figure? Can we do this by only looking at the position of corners in the dot grid?
Answer:
Given:
A collection of figures drawn on a dot paper grid.
Task:
Identify if there are any squares in the collection, using measurements if needed. Discuss reasoning about sides and angles using only dot positions.
Identifying Squares:
A square is a quadrilateral with four equal sides and four right angles ($90^\circ$). We can examine each figure by counting the number of units (spaces between dots) for the sides and observing the angles.
Let's analyze each figure:
- Figure 1 (Top Left): This figure has four sides connecting adjacent dots horizontally and vertically. Counting the spaces between dots, each side is 2 units long. The corners are formed by horizontal and vertical lines, which meet at right angles. Since all sides are equal and all angles are right angles, this figure is a square.
- Figure 2 (Top Middle): This figure has horizontal and vertical sides. The top and bottom sides are 3 units long. The left and right sides are 2 units long. The sides are not all equal. The angles are right angles (formed by horizontal and vertical lines). This is a rectangle, but not a square.
- Figure 3 (Top Right): This figure has four diagonal sides. Let's look at the 'run' (horizontal movement) and 'rise' (vertical movement) between the dots for each side. Each side moves 1 unit horizontally and 1 unit vertically between dots. The length of such a diagonal on a grid is $\sqrt{1^2 + 1^2} = \sqrt{2}$ units. Since all four sides have this same relative movement (1 unit horizontal, 1 unit vertical), all sides are equal in length. The angles formed at the vertices are where two diagonal lines meet. For example, at the top vertex, one side goes 1 unit right and 1 unit down, while the other goes 1 unit left and 1 unit down. These diagonal lines are perpendicular on a grid when their 'rise/run' values (slopes) are negative reciprocals. Here, the effective slopes relative to the grid axes are 1 and -1 (or -1 and 1). Since $1 \times (-1) = -1$, they meet at a right angle. All four angles are right angles. Since all sides are equal and all angles are right angles, this figure is a square.
- Figure 4 (Bottom Left): This figure has horizontal and diagonal sides. The top and bottom sides are 2 units long (horizontal). The left and right sides are diagonal, each moving 1 unit horizontally and 1 unit vertically. Their length is $\sqrt{2}$ units. The sides are not all equal. The angles are not right angles (e.g., the top-left angle is formed by a horizontal line and a diagonal line, which do not form a right angle in this configuration on a grid). This figure is not a square.
- Figure 5 (Bottom Right): This figure has four sides connecting adjacent dots horizontally and vertically. Counting the spaces between dots, each side is 3 units long. The corners are formed by horizontal and vertical lines, which meet at right angles. Since all sides are equal and all angles are right angles, this figure is a square.
Based on this analysis, the squares in this collection are Figure 1, Figure 3, and Figure 5.
Think: Reasoning without Measuring Instruments
Yes, it is possible to reason out if the sides are equal or not, and if the angles are right or not, without using any measuring instruments, by only looking at the position of corners in the dot grid.
Reasoning about equal sides:
For horizontal or vertical segments, we can simply count the number of unit spaces between the dots that form the side. If two horizontal segments have the same number of spaces, they are equal in length. The same applies to vertical segments.
For diagonal segments, we can look at the relative movement in the horizontal and vertical directions between the dots forming the segment. For example, a segment connecting dots that are 2 units apart horizontally and 1 unit apart vertically has a length of $\sqrt{2^2 + 1^2} = \sqrt{5}$ units. If two diagonal segments have the same horizontal 'run' and vertical 'rise' (regardless of direction), their lengths are equal. In Figure 3, all sides have a 'run' of 1 and a 'rise' of 1, so they are all equal in length.
Reasoning about right angles:
Angles formed by a horizontal line and a vertical line meeting on the grid are always right angles.
Angles involving diagonal lines can also be identified as right angles by looking at the grid pattern. Two lines are perpendicular if the product of their slopes is -1. On a dot grid, the "slope" between two dots can be thought of as the ratio of the vertical 'rise' to the horizontal 'run'. For lines forming a right angle on the grid, if one line has a 'rise' of $a$ and a 'run' of $b$, the perpendicular line will have a 'rise' of $b$ and a 'run' of $a$, but in opposite horizontal/vertical directions (e.g., if one goes (+a, +b), the other goes (+b, -a) or (-b, +a)). In Figure 3, each vertex connects two diagonal lines. For instance, at the top-right vertex, one side goes 1 unit left and 1 unit up (vector (-1, 1)), and the other goes 1 unit left and 1 unit down (vector (-1, -1)). The dot product $(-1)(-1) + (1)(-1) = 1 - 1 = 0$. A dot product of 0 means the vectors are perpendicular, confirming a right angle. This pattern of 'rise' and 'run' orthogonality can be visually confirmed on the grid without measuring.
In conclusion, by carefully observing the distances between dots (counting spaces) and the relative horizontal and vertical changes between connected dots (rise and run), we can determine side lengths and identify right angles to confirm if a figure is a square or not, without needing external measuring tools like a ruler or protractor.
Question 3. Draw at least 3 rotated squares and rectangles on a dot grid. Draw them such that their corners are on the dots. Verify if the squares and rectangles that you have drawn satisfy their respective properties.
Answer:
Properties of Squares and Rectangles:
- A square is a quadrilateral with four equal sides and four right angles.
- A rectangle is a quadrilateral with opposite sides equal and four right angles. (A square is a special type of rectangle where all sides are equal).
To draw rotated squares and rectangles on a dot grid such that their corners are on the dots, we need to choose sets of four dots that form the vertices of these shapes. The challenge is to ensure the sides are of the correct relative lengths and that adjacent sides are perpendicular (form right angles).
Drawing Rotated Squares on a Dot Grid:
For a square whose sides are not parallel to the grid lines, the sides will be diagonal. To ensure the sides are equal and the angles are right angles, the pattern of movement between consecutive vertices must follow a rule like $(a, b)$ then $(-b, a)$ then $(-a, -b)$ then $(b, -a)$, where $(a, b)$ represents moving 'a' units horizontally and 'b' units vertically between dots.
Here are steps for drawing three rotated squares:
Square 1 (Smallest rotated square with non-grid-aligned sides):
Movement pattern: (1 unit right, 1 unit up), then (1 unit left, 1 unit up), then (1 unit left, 1 unit down), then (1 unit right, 1 unit down).
1. Start at a dot (e.g., position (0,0) on the grid).
2. Move 1 unit right and 1 unit up to reach the next dot (position (1,1)). Draw the first side.
3. From (1,1), move 1 unit left and 1 unit up to reach the next dot (position (0,2)). Draw the second side.
4. From (0,2), move 1 unit left and 1 unit down to reach the next dot (position (-1,1)). Draw the third side.
5. From (-1,1), move 1 unit right and 1 unit down to return to the starting dot (position (0,0)). Draw the fourth side.
This forms a square rotated by $45^\circ$.
Square 2 (Larger rotated square):
Movement pattern: (2 units right, 1 unit up), then (1 unit left, 2 units up), then (2 units left, 1 unit down), then (1 unit right, 2 units down).
1. Start at a dot (e.g., (0,0)).
2. Move 2 units right and 1 unit up to (2,1). Draw side.
3. From (2,1), move 1 unit left and 2 units up to (1,3). Draw side.
4. From (1,3), move 2 units left and 1 unit down to (-1,2). Draw side.
5. From (-1,2), move 1 unit right and 2 units down to (0,0). Draw side.
Square 3 (Another rotated square):
Movement pattern: (1 unit right, 3 units up), then (3 units left, 1 unit up), then (1 unit left, 3 units down), then (3 units right, 1 unit down).
1. Start at a dot (e.g., (0,0)).
2. Move 1 unit right and 3 units up to (1,3). Draw side.
3. From (1,3), move 3 units left and 1 unit up to (-2,4). Draw side.
4. From (-2,4), move 1 unit left and 3 units down to (-3,1). Draw side.
5. From (-3,1), move 3 units right and 1 unit down to (0,0). Draw side.
Drawing Rotated Rectangles on a Dot Grid:
For a rotated rectangle, adjacent sides must be perpendicular, and opposite sides must be equal. The movement pattern between consecutive vertices could be $(a, b)$ then $(c, d)$ then $(-a, -b)$ then $(-c, -d)$, where $(a, b)$ and $(c, d)$ are movements for adjacent sides such that their dot product is 0 (meaning they are perpendicular) and the length of $(a, b)$ is different from the length of $(c, d)$. On a grid, simple perpendicular diagonal movements are $(a, b)$ and $(-b, a)$ (or $(b, -a)$). To make the lengths different, we can scale one of these vectors, e.g., $(a, b)$ and $k(-b, a)$ for some $k \ne 1$.
Here are steps for drawing two rotated rectangles:
Rectangle 1:
Adjacent movement patterns: (1 unit right, 2 units up) and (4 units left, 2 units up).
(Note: A movement of (4 left, 2 up) is vector (-4, 2). A movement of (1 right, 2 up) is vector (1, 2). Check perpendicularity: (1)(-4) + (2)(2) = -4 + 4 = 0. Perpendicular. Lengths $\sqrt{1^2+2^2}=\sqrt{5}$ and $\sqrt{(-4)^2+2^2}=\sqrt{16+4}=\sqrt{20}$. Lengths are different.)
1. Start at a dot (e.g., (0,0)).
2. Move 1 unit right and 2 units up to (1,2). Draw first side.
3. From (1,2), move 4 units left and 2 units up to (-3,4). Draw second side.
4. From (-3,4), move 1 unit left and 2 units down to (-4,2). Draw third side (opposite the first side, movement is $-(1,2) = (-1,-2)$... wait, my dot calculation is wrong).
Let's restart with vertices based on vectors: Start at $P_0$. $P_1 = P_0 + \vec{v_1}$, $P_2 = P_1 + \vec{v_2}$, $P_3 = P_2 - \vec{v_1}$, $P_4 = P_3 - \vec{v_2} = P_0$. Let $\vec{v_1} = (1, 2)$ and $\vec{v_2} = (-4, 2)$.
1. Start at (0,0).
2. Move 1 right, 2 up to (1,2). Draw side.
3. From (1,2), move 4 left, 2 up to (-3,4). Draw side.
4. From (-3,4), move 1 left, 2 down to (-4,2). Draw side.
5. From (-4,2), move 4 right, 2 down to (0,0). Draw side.
Vertices: (0,0), (1,2), (-3,4), (-4,2).
Rectangle 2:
Adjacent movement patterns: (3 units right, 1 unit up) and (2 units left, 6 units up).
(Note: Movement (3 right, 1 up) is (3, 1). Movement (2 left, 6 up) is (-2, 6). Check perpendicularity: (3)(-2) + (1)(6) = -6 + 6 = 0. Perpendicular. Lengths $\sqrt{3^2+1^2}=\sqrt{10}$ and $\sqrt{(-2)^2+6^2}=\sqrt{4+36}=\sqrt{40}$. Lengths are different.)
Let $\vec{v_1} = (3, 1)$ and $\vec{v_2} = (-2, 6)$.
1. Start at a dot (e.g., (0,0)).
2. Move 3 right, 1 up to (3,1). Draw side.
3. From (3,1), move 2 left, 6 up to (1,7). Draw side.
4. From (1,7), move 3 left, 1 down to (-2,6). Draw side.
5. From (-2,6), move 2 right, 6 down to (0,0). Draw side.
Vertices: (0,0), (3,1), (1,7), (-2,6).
Verification of Properties using the Dot Grid:
We can verify the properties of the drawn shapes by examining the positions of the dots (vertices) without using a ruler or protractor.
1. Verifying Side Lengths: For any side connecting two dots, determine the horizontal distance (run) and the vertical distance (rise) between the dots by counting the grid spaces. Let the run be $\Delta x$ and the rise be $\Delta y$. The length of the diagonal side is proportional to $\sqrt{(\Delta x)^2 + (\Delta y)^2}$. To check if sides are equal, compare the pairs of $(\Delta x, \Delta y)$ values (ignoring sign) for each side.
- For the squares, the $(\Delta x, \Delta y)$ pairs (ignoring direction) for all four sides should be the same (e.g., (1,1) for Square 1, (2,1) for Square 2, (1,3) for Square 3).
- For the rectangles, there should be two pairs of equal side lengths. Adjacent sides will have different lengths. The $(\Delta x, \Delta y)$ pair for one side should be equal to its opposite side, and the $(\Delta x, \Delta y)$ pair for an adjacent side should be equal to its opposite side (e.g., for Rectangle 1, adjacent sides have (1,2) and (4,2) as $(\Delta x, \Delta y)$ pairs, and opposite sides match these).
2. Verifying Right Angles: We need to check if adjacent sides are perpendicular. Consider two adjacent sides meeting at a vertex. Determine the $(\Delta x, \Delta y)$ movement from the vertex along each side. Let these movements be $(a, b)$ and $(c, d)$. If these sides form a right angle on the grid, the relationship $ac + bd = 0$ will hold.
- For grid-aligned lines (horizontal or vertical), perpendicularity is visually obvious (horizontal and vertical lines meet at right angles).
- For diagonal lines, check the 'rise' and 'run' relationship. If one side moves $(a, b)$ from the vertex, a perpendicular side moving from the same vertex will move $(-b, a)$ or $(b, -a)$. For example, in Square 2, from (0,0) we moved (2,1) and from (1,3) we moved (-2,1). The movements *relative to the shared vertex* need to be checked. Consider the vertex (1,3). The incoming side came from (2,1) (movement (-1, 2) from vertex). The outgoing side goes to (-1,2) (movement (-2, -1) from vertex). Check $(-1)(-2) + (2)(-1) = 2 - 2 = 0$. Thus, there is a right angle at (1,3). This pattern should hold for all four vertices.
- For Rectangle 1, at vertex (1,2), the incoming side came from (0,0) (movement (-1, -2) from vertex) and the outgoing side goes to (-3,4) (movement (-4, 2) from vertex). Check $(-1)(-4) + (-2)(2) = 4 - 4 = 0$. Right angle. This should hold for all vertices.
By using these visual inspection and counting techniques based on the dot grid structure, we can verify the side lengths and angles to confirm if the drawn shapes are indeed squares and rectangles.
Construct (Page 197)
Question 1. Draw a rectangle with sides of length 4 cm and 6 cm. After drawing, check if it satisfies both the rectangle properties.
Answer:
Given:
Sides of the rectangle with lengths 4 cm and 6 cm.
To Construct:
A rectangle with the given side lengths and verify its properties.
Properties of a Rectangle:
- Opposite sides are equal in length.
- All four angles are right angles ($90^\circ$).
Steps for Construction:
We will use a ruler and a protractor (or a set square) for this construction.
1. Draw a line segment AB of length 6 cm using a ruler.
2. At point A, use a protractor or set square to draw a ray AX perpendicular to AB. This ray forms a $90^\circ$ angle with AB.
3. Using a ruler, measure 4 cm along the ray AX from point A. Mark the point D such that AD = 4 cm.
4. Now, we need to find the fourth vertex, C. We know that BC must be parallel to AD and equal in length (4 cm), and DC must be parallel to AB and equal in length (6 cm).
One way to find C is:
- At point B, draw a ray BY perpendicular to AB using a protractor or set square.
- Using a ruler, measure 4 cm along the ray BY from point B. Mark the point C such that BC = 4 cm.
5. Join points D and C with a ruler. This forms the fourth side DC.
The figure ABCD is the constructed rectangle with sides AB = 6 cm, BC = 4 cm, AD = 4 cm, and CD = 6 cm, and angles at A and B are $90^\circ$.
Verification of Properties:
After constructing the rectangle ABCD, we need to check if it satisfies the properties:
1. Opposite sides are equal:
- Measure the length of side AB using a ruler. It should be 6 cm (as drawn).
- Measure the length of side DC using a ruler. It should also be 6 cm. Thus, AB = DC.
- Measure the length of side AD using a ruler. It should be 4 cm (as drawn).
- Measure the length of side BC using a ruler. It should also be 4 cm. Thus, AD = BC.
- The property of opposite sides being equal is satisfied.
2. All four angles are right angles:
- Use a protractor to measure $\angle \text{DAB}$. It was constructed as $90^\circ$.
- Use a protractor to measure $\angle \text{ABC}$. It was constructed as $90^\circ$.
- Measure $\angle \text{BCD}$ using a protractor. Since BC is parallel to AD and DC is parallel to AB, ABCD is a parallelogram. In a parallelogram, consecutive angles add up to $180^\circ$. Since $\angle \text{ABC} = 90^\circ$, $\angle \text{BCD} = 180^\circ - 90^\circ = 90^\circ$. You can verify this with a protractor.
- Measure $\angle \text{ADC}$ using a protractor. Similarly, since AD is parallel to BC and DC is parallel to AB, $\angle \text{ADC} = 180^\circ - \angle \text{DAB} = 180^\circ - 90^\circ = 90^\circ$. You can verify this with a protractor.
- The property of all four angles being right angles is satisfied.
Since the constructed figure ABCD has opposite sides equal and all four angles as right angles, it satisfies the properties of a rectangle.
Question 2. Draw a rectangle of sides 2 cm and 10 cm. After drawing, check if it satisfies both the rectangle properties.
Answer:
Given:
Sides of the rectangle with lengths 2 cm and 10 cm.
To Construct:
A rectangle with the given side lengths and verify its properties.
Properties of a Rectangle:
- Opposite sides are equal in length.
- All four angles are right angles ($90^\circ$).
Steps for Construction:
We will use a ruler and a protractor (or a set square) for this construction.
1. Draw a line segment AB of length 10 cm using a ruler.
2. At point A, use a protractor or set square to draw a ray AX perpendicular to AB. This ray forms a $90^\circ$ angle with AB.
3. Using a ruler, measure 2 cm along the ray AX from point A. Mark the point D such that AD = 2 cm.
4. Now, we need to find the fourth vertex, C. We know that BC must be parallel to AD and equal in length (2 cm), and DC must be parallel to AB and equal in length (10 cm).
One way to find C is:
- At point B, draw a ray BY perpendicular to AB using a protractor or set square.
- Using a ruler, measure 2 cm along the ray BY from point B. Mark the point C such that BC = 2 cm.
5. Join points D and C with a ruler. This forms the fourth side DC.
The figure ABCD is the constructed rectangle with sides AB = 10 cm, BC = 2 cm, AD = 2 cm, and CD = 10 cm, and angles at A and B are $90^\circ$.
Verification of Properties:
After constructing the rectangle ABCD, we need to check if it satisfies the properties:
1. Opposite sides are equal:
- Measure the length of side AB using a ruler. It should be 10 cm (as drawn).
- Measure the length of side DC using a ruler. It should also be 10 cm. Thus, AB = DC.
- Measure the length of side AD using a ruler. It should be 2 cm (as drawn).
- Measure the length of side BC using a ruler. It should also be 2 cm. Thus, AD = BC.
- The property of opposite sides being equal is satisfied.
2. All four angles are right angles:
- Use a protractor to measure $\angle \text{DAB}$. It was constructed as $90^\circ$.
- Use a protractor to measure $\angle \text{ABC}$. It was constructed as $90^\circ$.
- Measure $\angle \text{BCD}$ using a protractor. Since BC is parallel to AD and DC is parallel to AB, ABCD is a parallelogram. In a parallelogram, consecutive angles add up to $180^\circ$. Since $\angle \text{ABC} = 90^\circ$, $\angle \text{BCD} = 180^\circ - 90^\circ = 90^\circ$. You can verify this with a protractor.
- Measure $\angle \text{ADC}$ using a protractor. Similarly, since AD is parallel to BC and DC is parallel to AB, $\angle \text{ADC} = 180^\circ - \angle \text{DAB} = 180^\circ - 90^\circ = 90^\circ$. You can verify this with a protractor.
- The property of all four angles being right angles is satisfied.
Since the constructed figure ABCD has opposite sides equal and all four angles as right angles, it satisfies the properties of a rectangle.
Question 3. Is it possible to construct a 4-sided figure in which—
- all the angles are equal to 90º but
- opposite sides are not equal?
Answer:
Given Conditions:
- A 4-sided figure (quadrilateral).
- All the angles are equal to 90°.
- Opposite sides are not equal.
Analysis:
A quadrilateral with all four angles equal to 90° is defined as a rectangle.
Let the quadrilateral be ABCD, with angles $\angle \text{A} = \angle \text{B} = \angle \text{C} = \angle \text{D} = 90^\circ$.
In a quadrilateral, if the sum of consecutive interior angles is 180°, the lines are parallel.
- $\angle \text{A} + \angle \text{B} = 90^\circ + 90^\circ = 180^\circ$. This implies that side AD is parallel to side BC.
- $\angle \text{B} + \angle \text{C} = 90^\circ + 90^\circ = 180^\circ$. This implies that side AB is parallel to side DC.
Since both pairs of opposite sides are parallel (AD || BC and AB || DC), the quadrilateral ABCD is a parallelogram.
A fundamental property of all parallelograms is that their opposite sides are equal in length.
- Opposite sides AD and BC must be equal in length (AD = BC).
- Opposite sides AB and DC must be equal in length (AB = DC).
Therefore, any 4-sided figure with all angles equal to 90° must necessarily have its opposite sides equal.
Conclusion:
It is not possible to construct a 4-sided figure in which all the angles are equal to 90° but opposite sides are not equal.
The conditions "all angles are equal to 90°" and "opposite sides are not equal" are contradictory for a quadrilateral.
Construct (Page 199)
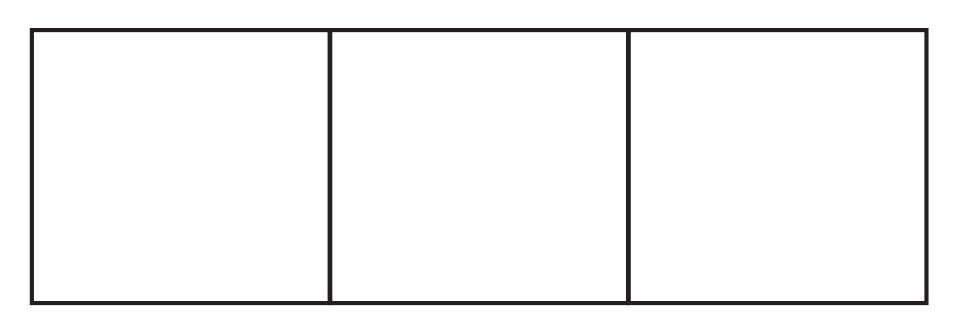
Construct a rectangle that can be divided into 3 identical squares as shown in the figure.
Answer:
Understanding the Figure:
The figure shows a rectangle that is divided into 3 identical squares placed side-by-side along the length of the rectangle.
This means that the length of the rectangle is equal to the sum of the side lengths of the three squares placed along the length, and the width of the rectangle is equal to the side length of one square.
Let 's' be the side length of each identical square. Then:
Length of the rectangle = $s + s + s = 3s$
Width of the rectangle = $s$
So, the dimensions of the rectangle must be in the ratio 3:1 (Length : Width).
To Construct:
A rectangle with dimensions such that its length is three times its width, and show how it can be divided into 3 identical squares.
Construction Required:
We need a ruler and a set square (or protractor) for this construction.
Let's choose a convenient side length for the squares, say $s = 3$ cm. Then the rectangle will have dimensions:
Width = 3 cm
Length = $3 \times 3$ cm = 9 cm
Steps for Construction of the Rectangle (9 cm by 3 cm):
1. Draw a line segment AB of length 9 cm using a ruler.
2. At point A, use a set square or protractor to draw a line segment AD perpendicular to AB, with length 3 cm. So, AD = 3 cm and $\angle \text{DAB} = 90^\circ$.
3. At point B, use a set square or protractor to draw a line segment BC perpendicular to AB, with length 3 cm. So, BC = 3 cm and $\angle \text{ABC} = 90^\circ$.
4. Join points D and C with a ruler. This forms the side DC.
The figure ABCD is the constructed rectangle with length AB = DC = 9 cm and width AD = BC = 3 cm. All angles are $90^\circ$ by construction.
Steps to Divide the Rectangle into 3 Identical Squares:
The side length of the identical squares is equal to the width of the rectangle, which is 3 cm.
1. On the side AB (length 9 cm), mark points P and Q such that AP = PQ = QB = 3 cm.
To do this, measure 3 cm from A along AB and mark point P. Then, measure 3 cm from P along PB and mark point Q.
2. From point P, draw a line segment parallel to AD (and BC), meeting DC at point R. Since AD is perpendicular to AB, this line PR will be perpendicular to AB and DC. The length of PR will be equal to AD = 3 cm.
3. From point Q, draw a line segment parallel to AD (and BC), meeting DC at point S. This line QS will be perpendicular to AB and DC, and its length will be equal to AD = 3 cm.
The rectangle ABCD is now divided into three smaller quadrilaterals: APQD, PQRS, and QBCR.
Let's check the dimensions of these quadrilaterals:
- APRD: AP = 3 cm, AD = 3 cm, DR (opposite AP) = 3 cm (since DC = 9 cm and DR = 9 - (3+3) = 3), PR = 3 cm. Angles at A and D are $90^\circ$. Since opposite sides are parallel and all sides are 3 cm and angles are $90^\circ$, APRD is a square of side 3 cm.
- PQRS: PQ = 3 cm, QR = 3 cm, RS = 3 cm (QS parallel to PR, S on DC), SP = 3 cm (PR parallel to QS, R on DC). Angles are $90^\circ$. So, PQRS is a square of side 3 cm.
- QBCR: QB = 3 cm, BC = 3 cm, CR = 3 cm, RQ = 3 cm. Angles are $90^\circ$. So, QBCR is a square of side 3 cm.
Thus, the rectangle of dimensions 9 cm by 3 cm can be divided into 3 identical squares of side 3 cm, as shown in the figure.
Question 2. Give the lengths of the sides of a rectangle that cannot be divided into —
- two identical squares;
- three identical squares.
Answer:
Let the side lengths of the rectangle be Length (L) and Width (W). We assume $L \ge W$.
Based on the figure provided in the previous question, when a rectangle is divided into identical squares arranged side-by-side along one dimension, the longer side of the rectangle must be an integer multiple of the shorter side, and the shorter side of the rectangle is equal to the side length of the square.
If a rectangle can be divided into two identical squares in this manner, its dimensions must be such that its Length is twice its Width (L = 2W).
If a rectangle can be divided into three identical squares in this manner, its dimensions must be such that its Length is three times its Width (L = 3W).
We are looking for a rectangle that cannot be divided into:
1. Two identical squares.
This means the length is not twice the width, i.e., $L \ne 2W$.
2. Three identical squares.
This means the length is not three times the width, i.e., $L \ne 3W$.
So, we need to find a pair of side lengths (L, W) such that $L \ne 2W$ and $L \ne 3W$. This is equivalent to saying that the ratio $\frac{L}{W}$ is not equal to 2 and is not equal to 3.
We can choose any pair of lengths where the ratio is not 2 or 3. For example, let's pick integer lengths.
Consider a rectangle with side lengths 4 cm and 3 cm.
Here, $L = 4$ cm and $W = 3$ cm (assuming the 4 cm side is the length).
Check for two identical squares:
Is $L = 2W$? Is $4 = 2 \times 3$? Is $4 = 6$? No.
So, a 4 cm by 3 cm rectangle cannot be divided into two identical squares (arranged side-by-side along the 4 cm side).
Check for three identical squares:
Is $L = 3W$? Is $4 = 3 \times 3$? Is $4 = 9$? No.
So, a 4 cm by 3 cm rectangle cannot be divided into three identical squares (arranged side-by-side along the 4 cm side).
Therefore, a rectangle with side lengths 4 cm and 3 cm cannot be divided into two identical squares or three identical squares.
Other possible pairs of side lengths include (5 cm, 2 cm), (5 cm, 3 cm), (7 cm, 4 cm), etc.
Construct (Page 201 - 203)
Question 1. A Square within a Rectangle
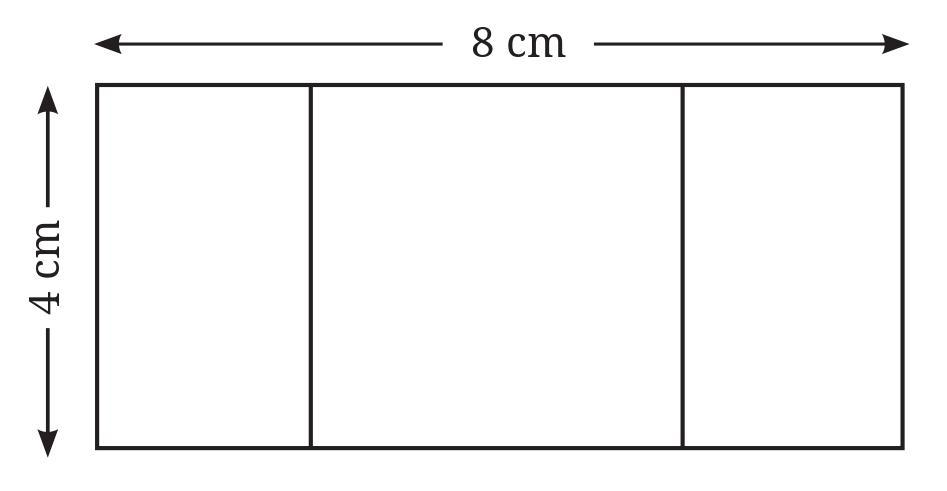
Construct a rectangle of sides 8 cm and 4 cm. How will you construct a square inside, as shown in the figure, such that the centre of the square is the same as the centre of the rectangle ?
Hint: Draw a rough figure. What will be the sidelength of the square? What will be the distance between the corners of the square and the outer rectangle?
Answer:
Given:
A rectangle with sides of length 8 cm and 4 cm.
To Construct:
A rectangle with the given dimensions and a square inside it such that the center of the square is the same as the center of the rectangle, as shown in the figure.
Construction Required:
Ruler, protractor (or set square).
Steps for Constructing the Rectangle (8 cm by 4 cm):
1. Draw a line segment AB of length 8 cm using a ruler.
2. At point A, use a protractor or set square to draw a ray AX perpendicular to AB. This ray forms a $90^\circ$ angle with AB.
3. Using a ruler, measure 4 cm along the ray AX from point A. Mark the point D such that AD = 4 cm.
4. At point B, use a protractor or set square to draw a ray BY perpendicular to AB. Using a ruler, measure 4 cm along the ray BY from point B. Mark the point C such that BC = 4 cm.
5. Join points D and C with a ruler. The figure ABCD is the constructed rectangle with sides AB = DC = 8 cm and AD = BC = 4 cm, and all angles are $90^\circ$.
Steps for Finding the Center of the Rectangle:
1. Draw the diagonals of the rectangle AC and BD using a ruler.
2. The point where the two diagonals intersect is the center of the rectangle. Mark this point as O.
Steps for Constructing the Square Inside:
The hint asks about the side length of the square and the distance from its corners to the outer rectangle. While the exact figure isn't provided, a common representation for a centered square inside a rectangle involves the square having its sides parallel to the rectangle's sides and a uniform 'margin' between the square and the rectangle edges (though the horizontal and vertical margins will differ if the rectangle is not a square). Let's assume from the implied figure that the inner square has a side length that allows for some margin on all sides.
A common side length used in such examples relative to an 8x4 rectangle that provides a margin is a 2 cm side length for the square. Let's assume the inner square has a side length of 2 cm.
1. We need to draw a square of side length 2 cm centered at point O with its sides parallel to the sides of the rectangle ABCD.
2. From the center O, measure half the side length of the square ($2 \text{ cm} \div 2 = 1 \text{ cm}$) along lines parallel and perpendicular to the rectangle's sides to find the vertices of the inner square.
Draw a horizontal line and a vertical line passing through O (these lines are parallel to the rectangle's sides).
From O, mark points 1 cm to the left, 1 cm to the right, 1 cm up, and 1 cm down along these lines.
Alternatively, measure 1 cm horizontally from O in both directions and 1 cm vertically from O in both directions. The four points obtained by combining these movements will be the vertices of the square.
- From O, move 1 cm left and 1 cm down. Mark the first vertex.
- From O, move 1 cm right and 1 cm down. Mark the second vertex.
- From O, move 1 cm right and 1 cm up. Mark the third vertex.
- From O, move 1 cm left and 1 cm up. Mark the fourth vertex.
3. Join the four marked vertices with a ruler. This forms the inner square.
Answering the Hint:
What will be the sidelength of the square?
Assuming the side length based on a typical figure, the side length of the square is 2 cm.
What will be the distance between the corners of the square and the outer rectangle?
Let's consider one corner of the inner square. Using the assumption of a 2x2 square centered in an 8x4 rectangle:
The center O is 4 cm from the 8 cm sides and 2 cm from the 4 cm sides of the rectangle.
The vertices of the 2x2 square are 1 cm horizontally and 1 cm vertically away from the center O.
Consider the top-right vertex of the inner square. Its horizontal distance from the center of the 8 cm length is 1 cm, and its vertical distance from the center of the 4 cm width is 1 cm.
The distance from this corner to the right vertical side of the rectangle (which is 4 cm from O horizontally) is $4 \text{ cm} - 1 \text{ cm} = 3 \text{ cm}$.
The distance from this corner to the top horizontal side of the rectangle (which is 2 cm from O vertically) is $2 \text{ cm} - 1 \text{ cm} = 1 \text{ cm}$.
So, the distance from each corner of the square to the nearest vertical side of the rectangle is 3 cm, and the distance from each corner to the nearest horizontal side of the rectangle is 1 cm.
Answer:
To construct the "Falling Squares" figure, we observe a pattern where a base square supports a layer of two smaller squares above it, which in turn support a layer of four even smaller squares, and so on. The side length of the squares is halved at each successive layer, and the squares in a layer are placed side-by-side along the top edge of the squares below them.
Construction Required:
Ruler, set square (or protractor), pencil.
Steps for Construction:
Let's assume we start with a base square of side length 's'. We can choose a convenient value for 's', like 8 cm or 8 units on a grid, to make divisions easier.
1. Draw the Base Square (Layer 1):
- Choose a point A as the bottom-left corner.
- Draw a horizontal line segment AB of length 's' using a ruler.
- At point A, draw a perpendicular line segment AD of length 's' upwards using a set square or protractor ($\angle \text{DAB} = 90^\circ$).
- At point B, draw a perpendicular line segment BC of length 's' upwards using a set square or protractor ($\angle \text{ABC} = 90^\circ$).
- Join points D and C. ABCD is the base square.
2. Construct the Second Layer (Two Squares):
- The second layer consists of two squares, each with a side length of $s/2$. These are placed side-by-side along the top edge DC of the base square.
- Find the midpoint M of the side DC. DM = MC = $s/2$.
- Draw a square with DM as its bottom side. Its vertices will be D, M, M', and D'. D' is vertically above D, and M' is vertically above M, both at a distance of $s/2$ from DC. Join D'M'.
- Draw a square with MC as its bottom side. Its vertices will be M, C, C', and M''. C' is vertically above C, and M'' is vertically above M, both at a distance of $s/2$ from DC. Join M''C'. (Note that M' and M'' are the same point).
- This creates two squares of side length $s/2$ above the base square. The top edges are D'M' and M'C'.
3. Construct the Third Layer (Four Squares):
- The third layer consists of four squares, each with a side length of $(s/2)/2 = s/4$. These are placed side-by-side along the top edges of the squares in the second layer (D'M' and M'C').
- Find the midpoint of D'M'. Let it be M1. D'M1 = M1M' = $s/4$.
- Find the midpoint of M'C'. Let it be M2. M'M2 = M2C' = $s/4$.
- Draw squares with D'M1, M1M', M'M2, and M2C' as their bottom sides. Their height will be $s/4$. For example, draw a square with D'M1 as the base. Its top edge will be $s/4$ directly above D'M1. Repeat for the other three segments.
- This creates four squares of side length $s/4$ in the third layer.
4. Construct the Fourth Layer (Eight Squares):
- The fourth layer consists of eight squares, each with a side length of $(s/4)/2 = s/8$. These are placed side-by-side along the top edges of the squares in the third layer.
- Find the midpoints of the top edges of the four squares in the third layer. Each top edge has length $s/4$, so the midpoints divide them into segments of length $s/8$.
- Draw squares of side length $s/8$ on each of these eight segments as their bottom sides.
You can continue this process to construct more layers, with the side length of the squares being halved in each subsequent layer ($s/16, s/32$, etc.). Due to the decreasing size, drawing more layers becomes challenging.
The figure is constructed by iteratively dividing the top edge of each square into two and building smaller squares on these segments upwards.
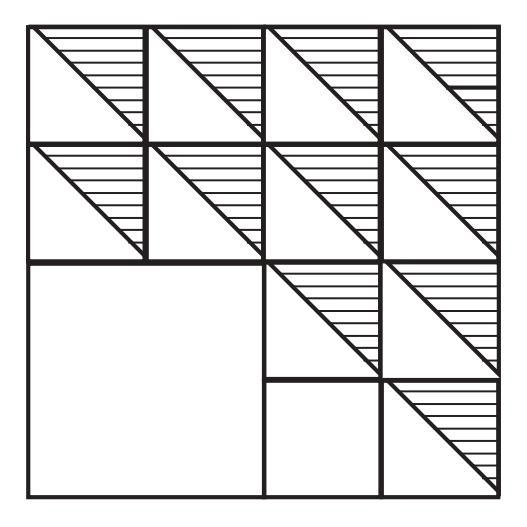
Construct this. Choose measurements of your choice. Note that the larger 4-sided figure is a square and so are the smaller ones.
Answer:
The given figure shows a large square divided into smaller regions, with certain regions shaded. We need to construct this figure by choosing our own measurements.
To Construct:
The shaded pattern within a large square, as shown in the given image.
Construction Steps:
Let's choose a convenient measurement for the side of the large square that is easily divisible. We can observe that the side of the large square is divided into $4$ equal parts in the figure. So, let's choose the side length to be $8$ cm.
1. Draw a large square and label its vertices as A, B, C, and D. Let the side length of this square be $8$ cm.
2. On each side of the square (AB, BC, CD, and DA), mark points that divide the side into four equal segments. Since the side is $8$ cm, each segment will be of length $8/4 = 2$ cm.
3. From the points marked on side AB, draw straight lines parallel to AD and BC, extending across the square to meet side CD. This will divide the square into four equal vertical strips.
4. From the points marked on side AD, draw straight lines parallel to AB and CD, extending across the square to meet side BC. This will divide the square into four equal horizontal strips.
5. These parallel lines create a grid of $4 \times 4 = 16$ smaller squares, each with a side length of $2$ cm.
6. Identify the central $2 \times 2$ block of these small squares. This forms a square with side length $2 \times 2$ cm $= 4$ cm. Shade this central $4$ cm $\times 4$ cm square.
7. Identify the four rectangular regions adjacent to the central shaded square, one on each side (top, bottom, left, right). Each of these rectangles is formed by a $1 \times 2$ block of the small squares. Their dimensions are $2$ cm $\times (2 \times 2)$ cm $= 2$ cm $\times 4$ cm. Shade these four $2$ cm $\times 4$ cm rectangles.
The resulting constructed figure will have the shaded pattern exactly as shown in the given image.
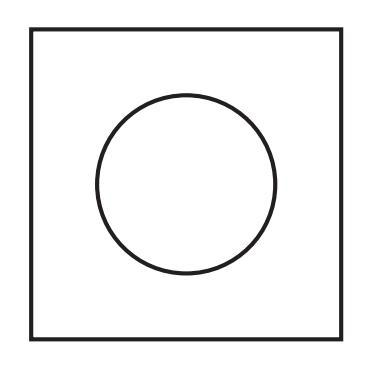
Hint: Think where the centre of the circle should be.
Answer:
The given figure shows a square with a large circle inscribed within it, and a smaller concentric circle inside the large one. The region between the two circles is shaded. We need to construct this figure by choosing our own measurements.
To Construct:
A square containing two concentric circles at its center, with the area between the circles shaded.
Construction Steps:
We need to choose a measurement for the side of the square. Let the side length of the square be $a$. The large circle inscribed in this square will have its diameter equal to the side length of the square, so its radius will be $R = a/2$. The smaller circular hole will be concentric with the large circle and the square, and it will have a radius $r < R$. Let's choose a convenient side length for the square that makes calculations simple, for example, $a = 10$ cm.
Therefore, the side length of the square is $10$ cm.
The radius of the large inscribed circle will be $R = 10/2 = 5$ cm.
Let's choose the radius of the smaller concentric circle (the hole) to be $r = 3$ cm (any value less than $5$ cm will work).
Now, let's perform the construction:
1. Draw a square ABCD with side length $10$ cm.
2. Find the center of the square. This is done by drawing the diagonals AC and BD. Let the point where the diagonals intersect be O. O is the center of the square and will be the common center for both circles.
3. With O as the center and radius $R = 5$ cm, draw a circle. This circle will be inscribed within the square, touching all four sides.
4. With O as the same center and radius $r = 3$ cm, draw another circle. This circle will be inside the first circle.
5. The required figure is the square ABCD with these two concentric circles drawn. The area to be shaded is the region that lies inside the circle with radius $5$ cm but outside the circle with radius $3$ cm.
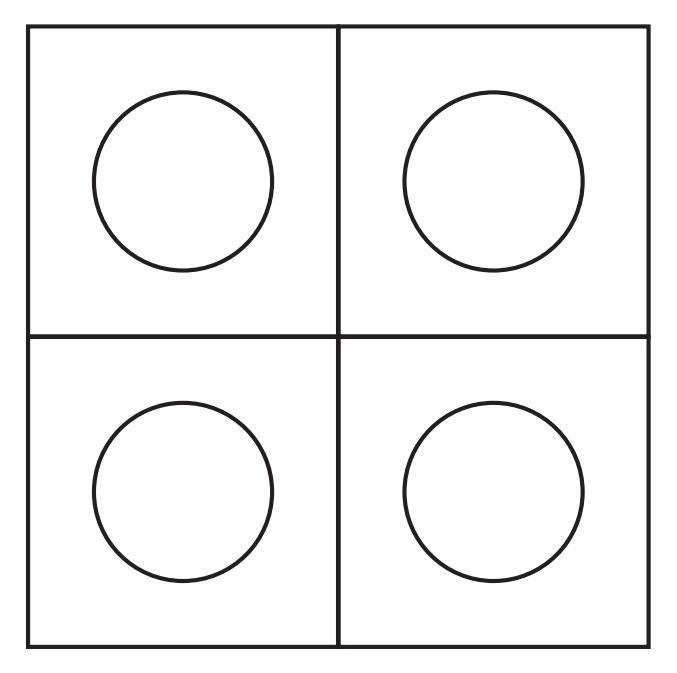
Answer:
The given figure shows a large square with four circular holes, one near each corner. The region within the square but outside the circular holes is shaded. We need to construct this figure by choosing our own measurements.
To Construct:
A large square containing four circular holes, symmetrically placed near the corners, with the area outside the circles shaded.
Construction Steps:
Let's choose a convenient measurement for the side of the large square. Observing the symmetry, it appears that the square can be conceptually divided into a $3 \times 3$ grid, and the centers of the circles are at the centers of the corner squares of this grid. Let's choose the side length of the large square to be $12$ cm for ease of division by 3.
So, the side length of the large square is $12$ cm.
If we divide the side into $3$ equal parts, each part will be $12/3 = 4$ cm long.
The center of each corner square in the $3 \times 3$ grid would be half the side length away from the edges of that square. Thus, the center of a corner square is $4/2 = 2$ cm away from the two adjacent sides of the large square.
The distance from the center of a corner square to the nearest edge of the large square is $2$ cm.
To have distinct circular holes, the radius of each circle must be less than this distance, i.e., less than $2$ cm. Let's choose the radius of each circle to be $1.5$ cm.
Now, let's perform the construction:
1. Draw a large square ABCD with side length $12$ cm.
2. On side AB, mark points P and Q such that AP = PQ = QB = $4$ cm. Similarly, mark points on sides BC, CD, and DA dividing them into $4$ cm segments.
3. Draw grid lines parallel to the sides through the marked points. This creates a $3 \times 3$ grid of smaller squares, each of side length $4$ cm.
4. Identify the centers of the four corner squares of this grid. For example, the center of the top-left square is $2$ cm from side AD and $2$ cm from side AB.
5. With the center of each of the four corner squares as the center, draw a circle with radius $1.5$ cm.
6. The required figure is the square ABCD with these four circular holes. The area to be shaded is the region within the square ABCD but outside the four circles.
Question 6. Square with Curves
This is a square with 8 cm sidelengths.
Hint: Think where the tip of the compass can be placed to get all the 4 arcs to bulge uniformly from each of the sides. Try it out!
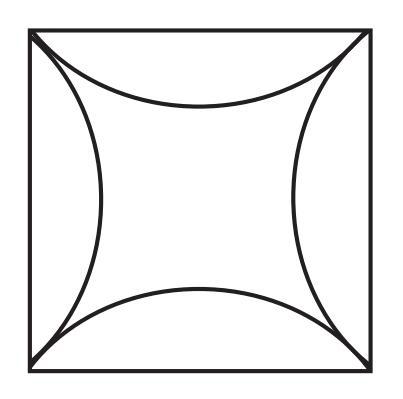
Answer:
The given figure shows a square with a shaded region in the center, bounded by four concave arcs. We are given that the side length of the square is $8$ cm. The hint suggests thinking about placing the compass tip to get the arcs that bulge uniformly from the sides.
Given:
A square with side length $8$ cm.
To Construct:
The shaded pattern within the square, as shown in the figure.
Construction Steps:
The shaded pattern is formed by four concave arcs connecting the adjacent vertices of the square and meeting in the center. Based on typical geometric constructions and the hint, these arcs are segments of circles whose centers are the vertices of the square, and the radius is equal to the side length of the square.
1. Draw a square ABCD with side length $8$ cm.
2. Set the compass radius to the side length of the square, which is $8$ cm.
3. Place the compass tip at vertex A. Draw an arc from vertex B to vertex D inside the square.
4. Place the compass tip at vertex B. Draw an arc from vertex C to vertex A inside the square.
5. Place the compass tip at vertex C. Draw an arc from vertex D to vertex B inside the square.
6. Place the compass tip at vertex D. Draw an arc from vertex A to vertex C inside the square.
7. The central region which is enclosed by these four arcs is the required shaded area. Shade this central region.
This construction creates four circular segments inside the square. The central region, which is the intersection of these four segments, forms the desired shaded pattern with concave arcs meeting near the center.
Construct (Page 211)
Question 1. Construct a rectangle in which one of the diagonals divides the opposite angles into 50° and 40°.
Answer:
We are asked to construct a rectangle where a diagonal splits the angles at the opposite vertices into $50^\circ$ and $40^\circ$. In a rectangle, all angles are $90^\circ$, and the sum of the parts $50^\circ + 40^\circ = 90^\circ$ is consistent.
Given:
A rectangle such that one of its diagonals divides the opposite angles into $50^\circ$ and $40^\circ$.
To Construct:
The rectangle satisfying the given condition.
Construction Steps:
Let the rectangle be ABCD and the diagonal be AC. The diagonal divides $\angle$A and $\angle$C into $50^\circ$ and $40^\circ$. Let's assume, without loss of generality, that $\angle$CAB = $40^\circ$ and $\angle$CAD = $50^\circ$. Due to alternate interior angles (since AB || DC), $\angle$ACD = $\angle$CAB = $40^\circ$. Also, since AD || BC, $\angle$ACB = $\angle$CAD = $50^\circ$. The point of intersection of the diagonals is the center of the rectangle, and the diagonals of a rectangle are equal and bisect each other. Let the intersection point be O. In $\triangle$AOB, OA = OB (half diagonals are equal), so it is an isosceles triangle. $\angle$OAB = $\angle$CAB = $40^\circ$. Thus, $\angle$OBA = $40^\circ$. The angle between the diagonals $\angle$AOB = $180^\circ - (\angle$OAB + $\angle$OBA$) = 180^\circ - (40^\circ + 40^\circ) = 180^\circ - 80^\circ = 100^\circ$. We can use this angle to construct the rectangle.
1. Draw a line segment AC of any convenient length (e.g., $8$ cm). This will be one diagonal of the rectangle.
2. Find the midpoint O of AC. You can do this by drawing the perpendicular bisector of AC or by measuring half the length from either end.
3. At point O, construct an angle equal to $100^\circ$. Draw a line through O at this angle to AC. Let this line be XOY.
4. With O as the center and radius equal to OA (which is half the length of AC, i.e., $4$ cm if AC was $8$ cm), draw arcs intersecting the line XOY at points B and D. Make sure B and D are on opposite sides of O.
5. Join points A to B, B to C, C to D, and D to A.
Justification:
By construction, the diagonals AC and BD intersect at O and bisect each other (OA=OC and OB=OD). Also, we made OA=OB=OC=OD by using the same radius from O. This implies that ABCD is a rectangle.
The angle between the diagonals $\angle$AOB is constructed as $100^\circ$.
In $\triangle$AOB, OA = OB, so it is isosceles. $\angle$OAB = $\angle$OBA = $(180^\circ - 100^\circ)/2 = 80^\circ/2 = 40^\circ$. Thus, $\angle$CAB = $40^\circ$.
$\angle$BOC = $180^\circ - \angle$AOB = $180^\circ - 100^\circ = 80^\circ$.
In $\triangle$BOC, OB = OC, so it is isosceles. $\angle$OBC = $\angle$OCB = $(180^\circ - 80^\circ)/2 = 100^\circ/2 = 50^\circ$. Thus, $\angle$BCA = $50^\circ$.
The angle at vertex B is $\angle$ABC = $\angle$OBA + $\angle$OBC = $40^\circ + 50^\circ = 90^\circ$. Similarly, angles at A, C, and D are $90^\circ$. Thus, ABCD is a rectangle.
The diagonal AC divides $\angle$DAB into $\angle$CAB and $\angle$CAD. We found $\angle$CAB = $40^\circ$. In $\triangle$AOD, OA = OD, $\angle$AOD = $80^\circ$. $\angle$OAD = $(180^\circ - 80^\circ)/2 = 50^\circ$. So $\angle$CAD = $50^\circ$. The parts are $40^\circ$ and $50^\circ$.
The diagonal AC divides $\angle$BCD into $\angle$BCA and $\angle$ACD. We found $\angle$BCA = $50^\circ$. In $\triangle$DOC, OC = OD, $\angle$DOC = $100^\circ$. $\angle$OCD = $(180^\circ - 100^\circ)/2 = 40^\circ$. So $\angle$ACD = $40^\circ$. The parts are $50^\circ$ and $40^\circ$.
Thus, the constructed figure is a rectangle where the diagonal divides the opposite angles into $50^\circ$ and $40^\circ$.
Question 2. Construct a rectangle in which one of the diagonals divides the opposite angles into 45° and 45°. What do you observe about the sides?
Answer:
We are asked to construct a rectangle where a diagonal splits the angles at the opposite vertices into $45^\circ$ and $45^\circ$. In a rectangle, each angle is $90^\circ$. Dividing a $90^\circ$ angle into $45^\circ$ and $45^\circ$ means the diagonal bisects the angle.
Given:
A rectangle such that one of its diagonals divides the opposite angles into $45^\circ$ and $45^\circ$.
To Construct:
The rectangle satisfying the given condition and observe the nature of its sides.
Construction Steps:
Let the rectangle be ABCD and the diagonal be AC. The diagonal divides $\angle$A and $\angle$C into $45^\circ$ and $45^\circ$. This means $\angle$BAC = $45^\circ$ and $\angle$CAD = $45^\circ$, and $\angle$BCA = $45^\circ$ and $\angle$DCA = $45^\circ$.
Let's choose a convenient side length for the rectangle. Since the angles formed by the diagonal are $45^\circ$, this suggests a special type of rectangle. Let's proceed by constructing a side and then the angles.
1. Draw a line segment AB of any convenient length, say $a$ units.
2. At point A, construct a ray AX making an angle of $45^\circ$ with AB such that $\angle$BAX = $45^\circ$.
3. At point B, construct a ray BY such that BY is perpendicular to AB. So $\angle$ABY = $90^\circ$.
4. The diagonal AC lies on the ray AX. Since $\angle$BAC = $45^\circ$ and $\angle$ABC = $90^\circ$, in $\triangle$ABC, $\angle$BCA = $180^\circ - 90^\circ - 45^\circ = 45^\circ$.
5. Since $\angle$BCA = $45^\circ$, the side BC must have the same length as AB (because $\triangle$ABC is an isosceles right-angled triangle with $\angle$BAC = $\angle$BCA = $45^\circ$). So, measure the length of AB ($a$) and mark a point C on the ray BY such that BC = $a$ units.
6. Now, we need to find point D. Since ABCD is a rectangle, AD must be parallel to BC and CD must be parallel to AB. Also, AD must be perpendicular to AB and CD must be perpendicular to BC.
7. At point C, construct a ray CZ perpendicular to BC. Mark a point D on this ray such that CD = AB = $a$ units.
8. Join points A and D.
The figure ABCD is the required rectangle.
Observation about the sides:
In the construction, we made BC = AB = $a$. In a rectangle, opposite sides are equal, so CD = AB = $a$ and AD = BC = $a$.
Thus, we observe that all four sides of the rectangle are equal in length:
AB = BC = CD = DA
A rectangle with all sides equal is a square.
Therefore, a rectangle in which one of the diagonals divides the opposite angles into $45^\circ$ and $45^\circ$ is a square.
Question 3. Construct a rectangle one of whose sides is 4 cm and the diagonal is of length 8 cm.
Answer:
We are asked to construct a rectangle given the length of one side and the length of its diagonal.
Given:
A rectangle with one side of length $4$ cm and a diagonal of length $8$ cm.
To Construct:
The rectangle satisfying the given conditions.
Construction Steps:
Let the rectangle be ABCD. Let the given side be AB $= 4$ cm and the diagonal be AC $= 8$ cm. Since ABCD is a rectangle, $\angle$ABC $= 90^\circ$. Thus, $\triangle$ABC is a right-angled triangle with hypotenuse AC and one leg AB.
1. Draw a line segment AB of length $4$ cm.
2. At point B, construct a ray BX perpendicular to AB. This ray will contain the side BC.
3. With A as the center and radius equal to the length of the diagonal ($8$ cm), draw an arc that intersects the ray BX at point C.
4. At point A, construct a ray AY perpendicular to AB. This ray will contain the side AD.
5. We know that opposite sides of a rectangle are equal. So, CD must be equal to AB ($4$ cm) and AD must be equal to BC. To find point D, with C as the center and radius $4$ cm, draw an arc.
6. This arc should intersect the ray AY at point D.
7. Join points C and D.
The figure ABCD is the required rectangle.
Justification:
By construction, AB $= 4$ cm and AC $= 8$ cm. $\angle$ABC $= 90^\circ$. Thus, $\triangle$ABC is a right-angled triangle. BC is determined by the intersection of the arc from A and the perpendicular at B. By Pythagorean theorem, $AB^2 + BC^2 = AC^2 \implies 4^2 + BC^2 = 8^2 \implies 16 + BC^2 = 64 \implies BC^2 = 48 \implies BC = \sqrt{48} = 4\sqrt{3}$ cm. The length of side BC is $4\sqrt{3}$ cm.
Also by construction, $\angle$BAD $= 90^\circ$. CD $= 4$ cm (radius of arc from C). Since AD is on the ray AY perpendicular to AB and CD is drawn from C with length 4 cm, and D is on AY, ABCD forms a parallelogram with right angles at A and B. Since it has right angles, it is a rectangle. Also, AD will be equal to BC ($4\sqrt{3}$ cm) and CD will be equal to AB ($4$ cm), satisfying the property of opposite sides being equal in a rectangle.
Question 4. Construct a rectangle one of whose sides is 3 cm and the diagonal is of length 7 cm.
Answer:
We are asked to construct a rectangle given the length of one side and the length of its diagonal.
Given:
A rectangle with one side of length $3$ cm and a diagonal of length $7$ cm.
To Construct:
The rectangle satisfying the given conditions.
Construction Steps:
Let the rectangle be ABCD. Let the given side be AB $= 3$ cm and the diagonal be AC $= 7$ cm. Since ABCD is a rectangle, $\angle$ABC $= 90^\circ$. Thus, $\triangle$ABC is a right-angled triangle with hypotenuse AC and one leg AB.
1. Draw a line segment AB of length $3$ cm.
2. At point B, construct a ray BX perpendicular to AB. This ray will contain the side BC.
3. With A as the center and radius equal to the length of the diagonal ($7$ cm), draw an arc that intersects the ray BX at point C.
4. At point A, construct a ray AY perpendicular to AB. This ray will contain the side AD.
5. We know that opposite sides of a rectangle are equal. So, CD must be equal to AB ($3$ cm) and AD must be equal to BC. To find point D, with C as the center and radius $3$ cm, draw an arc.
6. This arc should intersect the ray AY at point D.
7. Join points C and D.
The figure ABCD is the required rectangle.
Justification:
By construction, AB $= 3$ cm and AC $= 7$ cm. $\angle$ABC $= 90^\circ$. Thus, $\triangle$ABC is a right-angled triangle. BC is determined by the intersection of the arc from A and the perpendicular at B. By Pythagorean theorem, $AB^2 + BC^2 = AC^2$.
$(3)^2 + BC^2 = (7)^2$
... (i)
$9 + BC^2 = 49$
$BC^2 = 49 - 9 = 40$
$BC = \sqrt{40} = 2\sqrt{10}$ cm
The length of side BC is $2\sqrt{10}$ cm.
Also by construction, $\angle$BAD $= 90^\circ$. CD $= 3$ cm (radius of arc from C). Since AD is on the ray AY perpendicular to AB and CD is drawn from C with length 3 cm, and D is on AY, ABCD forms a parallelogram with right angles at A and B. Since it has right angles, it is a rectangle. Also, AD will be equal to BC ($2\sqrt{10}$ cm) and CD will be equal to AB ($3$ cm), satisfying the property of opposite sides being equal in a rectangle.
Construct (Page 215)
Answer:
The image shows a simple house shape consisting of a square base and a triangular roof, with a door and a window drawn inside the base. We are asked to construct a "bigger house" where "all the sides are of length 7 cm". This phrasing likely refers to the main external sides of the house shape (the sides of the square base and the sloping sides of the roof). The roof appears to be an equilateral triangle based on the context of simple constructions and the uniform length requirement.
To Construct:
A figure representing a house with a square base of side length $7$ cm and an equilateral triangular roof of side length $7$ cm, including a door and a window proportional to the original figure.
Construction Steps:
We will construct the square base first, then the equilateral triangular roof on top, and finally add the door and window based on reasonable proportions from the provided image.
1. Draw a line segment AB of length $7$ cm. This will be the base of the square.
2. At point A, construct a ray perpendicular to AB extending upwards.
3. At point B, construct a ray perpendicular to AB extending upwards.
4. With A as the center and radius $7$ cm, draw an arc that intersects the perpendicular ray from A. Mark the intersection point as D.
5. With B as the center and radius $7$ cm, draw an arc that intersects the perpendicular ray from B. Mark the intersection point as C.
6. Join points D and C. ABCD is the square base with side length $7$ cm.
7. Now, construct the equilateral triangle roof on the side DC. With D as the center and radius $7$ cm, draw an arc above the segment DC.
8. With C as the center and radius $7$ cm, draw an arc above the segment DC. The intersection of these two arcs is the vertex E (the peak of the roof).
9. Join D to E and C to E. Triangle DCE is the equilateral triangle roof.
10. Construct the door: Based on the visual proportion in the original image, the door seems to be roughly $\frac{1}{4}$ the width of the base and about half the height. Let's make the door width $2$ cm and height $3.5$ cm, centered on the base AB. On AB, mark point P such that AP = $\frac{7-2}{2} = 2.5$ cm. Mark point Q on AB such that AQ = $2.5 + 2 = 4.5$ cm.
11. At P, construct a perpendicular segment upwards of length $3.5$ cm and label the endpoint R.
12. At Q, construct a perpendicular segment upwards of length $3.5$ cm and label the endpoint S.
13. Join R to S. PQSR is the rectangular door.
14. Construct the window: The window in the image appears to be a square, centered above the door. Let's make it a $2$ cm $\times 2$ cm square, placed $1$ cm above the door. The top of the door is at height $3.5$ cm from AB. So the bottom of the window will be at height $3.5 + 1 = 4.5$ cm from AB. The window is horizontally centered, like the door. The left edge will be at $2.5$ cm from the left side of the square (AD).
15. From point A, measure $4.5$ cm upwards along AD and mark a temporary point. From this point, measure $2.5$ cm horizontally towards the right and mark point V. V is the bottom-left corner of the window.
16. From V, draw a vertical segment VW upwards of length $2$ cm.
17. From W, draw a horizontal segment WX to the right of length $2$ cm.
18. From X, draw a vertical segment XY downwards of length $2$ cm.
19. Join Y to V. VWXY is the square window.
The figure ABCE with the door PQSR and window VWXY represents the constructed bigger house.
Question 2. Try to recreate ‘A Person’, ‘Wavy Wave’ and ‘Eyes’ from the section Artwork, using ideas involved in the ‘House’ construction.
Answer:
The 'House' construction primarily involved combining basic geometric shapes (square, equilateral triangle) by drawing lines and using a compass to mark lengths and construct angles ($90^\circ$ and implied $60^\circ$ in the equilateral triangle). It also involved adding internal features (door, window) by measuring distances and drawing smaller shapes. We can use similar ideas to recreate the other figures.
Recreating 'A Person':
This figure likely represents a simplified human form using basic shapes like rectangles/squares and circles, connected by lines (limbs). We can choose simple measurements, similar to how we chose side lengths for the house.
To Construct:
A figure resembling a person, composed of simple geometric shapes.
Construction Steps:
Let's construct the body first, then the head, and finally the limbs.
1. Draw a vertical line segment representing the torso. Let its length be $4$ cm.
2. At the top endpoint of this segment, draw a circle representing the head. Let the radius be $1$ cm. The center of the circle can be placed just above the torso line endpoint.
3. From the top endpoint of the torso, draw two line segments extending sideways and slightly downwards, representing the arms. Let each arm be $3$ cm long.
4. From the bottom endpoint of the torso, draw two line segments extending downwards, representing the legs. Let each leg be $4$ cm long.
Alternatively, we could make the body a rectangle or square as shown in some simple diagrams:
1. Draw a rectangle for the body, say $3$ cm wide and $4$ cm tall.
2. Find the center of the top side of the rectangle.
3. From this center, draw a circle of radius $1$ cm, placed just above the rectangle's top edge, for the head.
4. From the points roughly $\frac{1}{4}$ of the way down from the top corners of the rectangle, draw line segments for arms, say $3$ cm long.
5. From the bottom corners of the rectangle, draw line segments downwards for legs, say $4$ cm long.
Recreating 'Wavy Wave':
This figure is formed by a series of connected arcs. This uses the idea of drawing arcs with a compass, similar to finding the peak of the roof in the house construction.
To Construct:
A wavy line composed of connected arcs.
Construction Steps:
We can create a wavy line by drawing alternating arcs from centers positioned above and below a base line.
1. Draw a horizontal base line. Mark several points along this line at equal distances, say $2$ cm apart. Label them $P_1, P_2, P_3, P_4, ...$
2. Choose a radius for the arcs, say $2.5$ cm.
3. Choose a point above the base line, say $C_1$, such that the distance from $C_1$ to $P_1$ and $P_2$ is equal to the chosen radius ($2.5$ cm). You can find $C_1$ by drawing arcs of radius $2.5$ cm centered at $P_1$ and $P_2$ and finding their intersection point above the line.
4. With $C_1$ as the center and radius $2.5$ cm, draw an arc connecting $P_1$ and $P_2$. This forms the first upward curve.
5. Choose a point below the base line, say $C_2$, such that the distance from $C_2$ to $P_2$ and $P_3$ is equal to the chosen radius ($2.5$ cm). Find $C_2$ by drawing arcs from $P_2$ and $P_3$ below the line.
6. With $C_2$ as the center and radius $2.5$ cm, draw an arc connecting $P_2$ and $P_3$. This forms the first downward curve.
7. Continue this pattern, alternating the center position (above/below the line) and drawing arcs between consecutive points on the base line ($P_3-P_4$, $P_4-P_5$, etc.) using the same radius.
Connecting these arcs creates the wavy line.
Recreating 'Eyes':
This figure likely shows two eye shapes, possibly simplified as circles or arcs. The simplest interpretation using basic tools is drawing circles.
To Construct:
A figure representing eyes, using circles or arcs.
Construction Steps (using Circles):
This involves drawing circles with a chosen radius and positioning them appropriately.
1. Draw a horizontal line segment of a convenient length, say $6$ cm. Mark its midpoint M.
2. From M, measure $1.5$ cm to the left and mark point $O_1$. From M, measure $1.5$ cm to the right and mark point $O_2$. $O_1$ and $O_2$ will be the centers of the eyes.
3. Choose a radius for the outer eye shape, say $1$ cm.
4. With $O_1$ as the center and radius $1$ cm, draw a circle.
5. With $O_2$ as the center and radius $1$ cm, draw a circle.
6. Now, add the pupils/irises. Choose a smaller radius, say $0.5$ cm.
7. With $O_1$ as the center and radius $0.5$ cm, draw a circle inside the first circle.
8. With $O_2$ as the center and radius $0.5$ cm, draw a circle inside the second circle.
This construction creates two identical eyes as concentric circles, placed symmetrically, similar to placing the door and window in the house based on measurements and position.
Question 3. Is there a 4-sided figure in which all the sides are equal in length but is not a square? If such a figure exists, can you construct it?
Answer:
Yes, such a 4-sided figure exists. A 4-sided figure in which all sides are equal in length is called a rhombus.
A square is a special type of rhombus where all angles are $90^\circ$. A rhombus that is not a square has all sides equal, but its angles are not all equal to $90^\circ$. Opposite angles of a rhombus are equal, and adjacent angles are supplementary (their sum is $180^\circ$).
To Construct:
A rhombus that is not a square.
Construction Steps:
We can construct a rhombus by choosing a side length and an angle (other than $90^\circ$) between two adjacent sides. Let's choose the side length to be $5$ cm and one angle to be $60^\circ$.
1. Draw a line segment AB of length $5$ cm.
2. At point A, construct an angle of $60^\circ$. Draw a ray AX along this angle.
3. With A as the center and radius $5$ cm, draw an arc intersecting the ray AX at point D.
4. Now we need to find point C. C is $5$ cm away from B and $5$ cm away from D (since all sides of a rhombus are equal).
5. With B as the center and radius $5$ cm, draw an arc.
6. With D as the center and radius $5$ cm, draw another arc. The intersection of these two arcs is point C.
7. Join points B to C and D to C.
The figure ABCD is a rhombus.
Justification:
By construction, AB = AD = $5$ cm. Also, BC = DC = $5$ cm (from the compass arcs). Therefore, AB = BC = CD = DA = $5$ cm. All sides are equal.
However, the angle $\angle$BAD is constructed as $60^\circ$, which is not $90^\circ$. Therefore, the figure is a rhombus but not a square.
The angles of the rhombus are: $\angle$BAD $= 60^\circ$. Since opposite angles in a rhombus are equal, $\angle$BCD $= 60^\circ$. Adjacent angles are supplementary, so $\angle$ABC $= 180^\circ - 60^\circ = 120^\circ$, and $\angle$ADC $= 180^\circ - 60^\circ = 120^\circ$.

